El terrible aprendizaje de la geometría
Aprender geometría no es nada fácil.
De hecho, es una tarea mucho más compleja que, por ejemplo, aprender sobre números u operaciones aritméticas.
Pero ¿por qué resulta tan difícil?
Esta pregunta se la hicieron hace 60 años dos personas: Dina van Hiele-Geldorf y Pierre van Hiele.
Ellos se lo tomaron muy en serio y decidieron hacer dos tesis doctorales para encontrar alguna respuesta.
Y la hallaron.
Sus tesis dieron lugar a lo que se denomina el Modelo de van Hiele. Una teoría ampliamente aceptada de enseñanza y aprendizaje de la geometría.
Los Van Hiele, determinaron cinco niveles de aprendizaje geométrico.
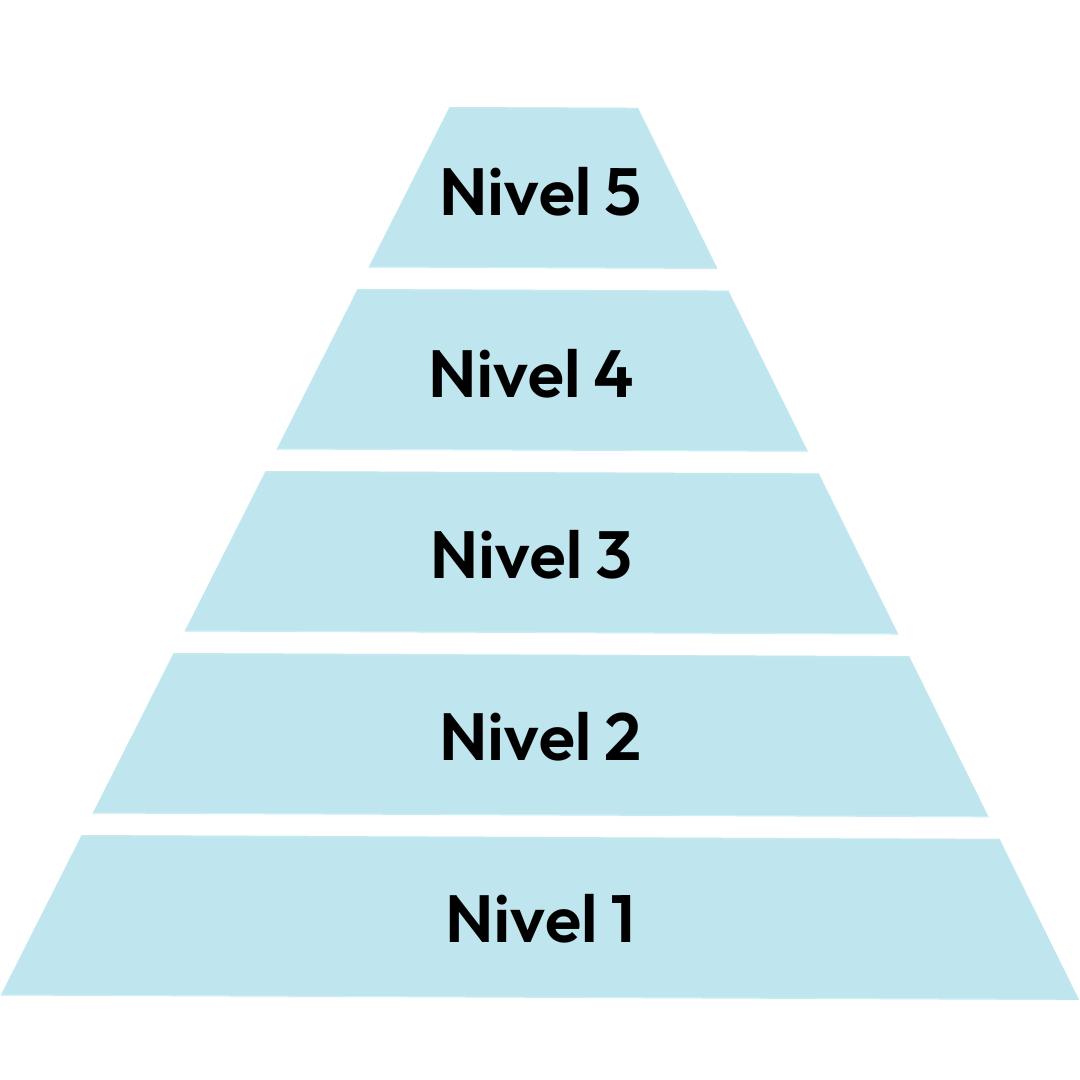
Algo que resulta sorprendente es que estos grados no van asociados a la edad sino que dependen de haber alcanzado el nivel previo.
Te quiero mostrar cómo son esos niveles con un ejemplo.
El primer nivel es el de Visualización o Reconocimiento.
En él, los estudiantes ven las figuras globalmente, sin fijarse en sus características. Dicen frases como «tiene forma de triángulo», «parece un cuadrado» o «es como un rombo»…
Muchas personas se quedan en este nivel toda la vida. Aunque hayan estudiado geometría en la escuela o en el instituto, no han pasado de la fase de Visualización.
Cuando ven un cuadrado dibujado “como un rombo”, es decir, apoyado sobre un vértice, dicen que es un rombo.

El segundo nivel es el de Análisis.
Una persona en este nivel es capaz de analizar el rombo y el cuadrado.
Ve características similares en ellos: son figuras planas formadas por rectas (son polígonos), tienen cuatro lados (son cuadriláteros) y todos sus lados son de la misma longitud (son equiláteros).
Pero también se fija en una gran diferencia: el cuadrado tiene los cuatro ángulos rectos y el rombo no.
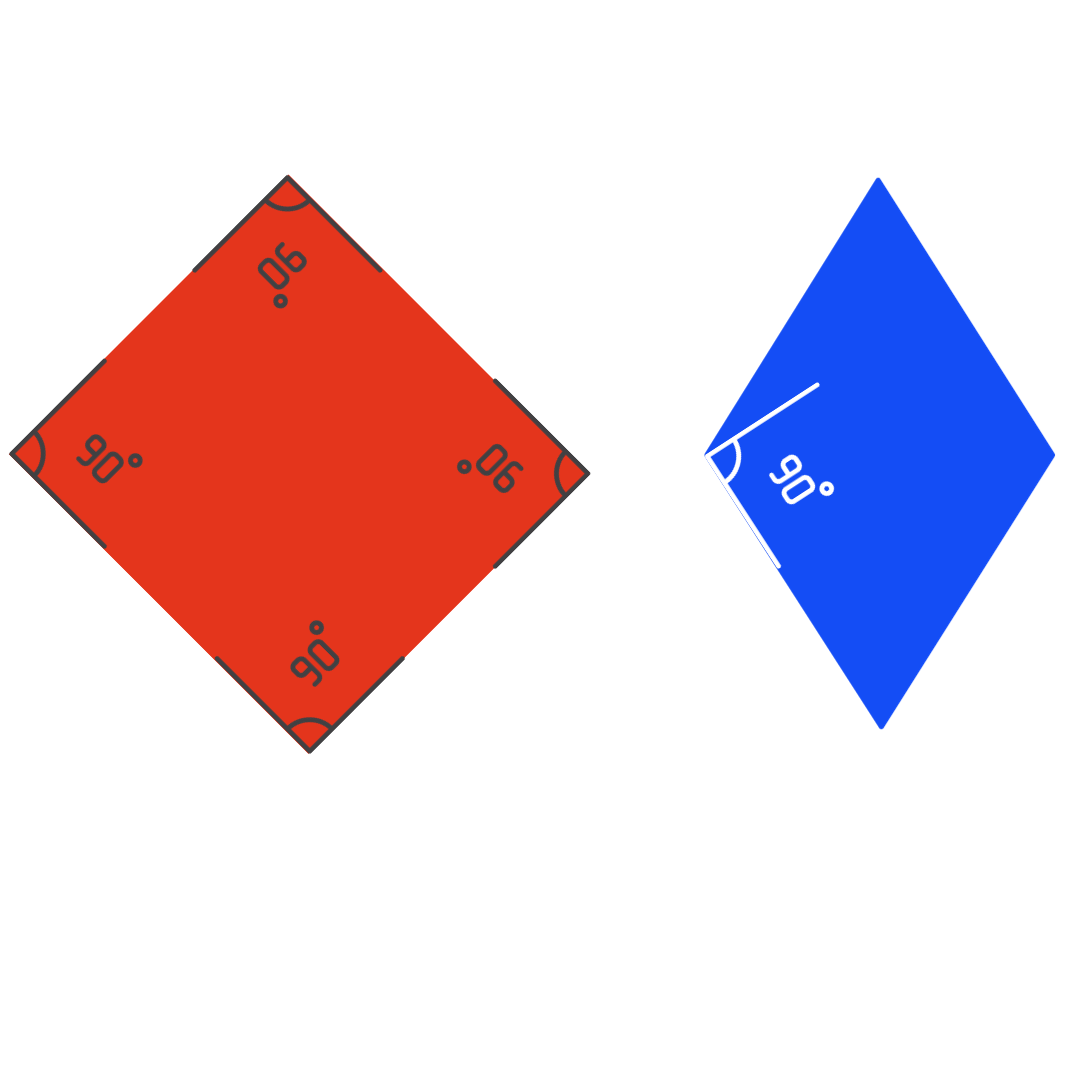
Sigo.
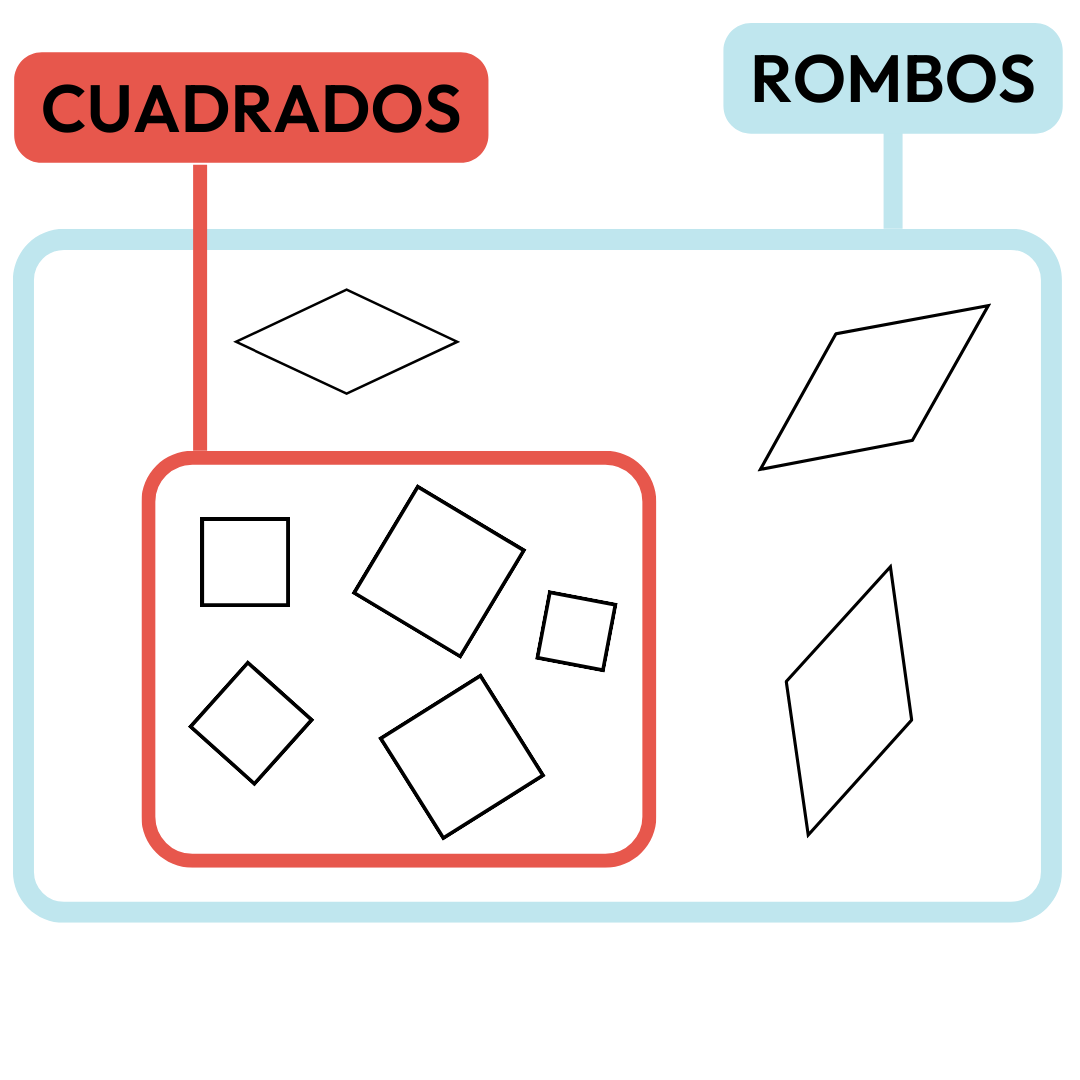
Un estudiante en un nivel 3, Ordenación o Clasificación, podría afirmar que el cuadrado es un tipo de rombo porque cumple todas las condiciones del rombo y una más (tener cuatro ángulos rectos).
Es decir, podría clasificar al cuadrado dentro del conjunto de los rombos.
De hecho, podrías decir que un cuadrado es un rombo. Pero, ojo, no por como está dibujado sino razonando que cumple las mismas propiedades.
Durante la Primaria y la Secundaria, los niños tienen que ir progresando por estos tres niveles.
Quedan dos más pero al ser más complejos son adecuados en Bachillerato o matemáticas universitarias.
Acabo de mostrarte cómo un estudiante debería ir avanzando desde una idea ingenua de un cuadrado y un rombo hasta una noción geométrica abstracta.
Fíjate que sin embargo en la escuela seguimos trabajando a partir de consignas como:
Preguntas descontextualizadas, normalmente a partir de figuras geométricas dibujadas en los libros, en la pizarra o en el ordenador. Actividades que perpetúan un terrible aprendizaje de la geometría en todas las edades.
La geometría requiere un grado de observación, de análisis y reflexión mucho más profundo del que habitualmente se propone en los libros de texto.
Ahora una pregunta lógica puede ser:
Entonces, ¿qué puedes hacer para que los niños avancen por los niveles de razonamiento geométrico?
¿Cómo puedes evitar que se estanquen en un nivel?
Ya te adelanto que no es siguiendo los dibujos o esquemas de un libro de texto ni haciéndoles asociar la forma al nombre de una figura ni, por supuesto, exigiéndoles que se memoricen fórmulas que no entienden.
Y otra cosa que quiero dejar clara: aprender geometría nunca debería ser un mero trámite.
Porque si los niños NO aprenden bien geometría:
Lo bueno, es que para que realmente avancen y que la geometría pase de ser un aprendizaje anecdótico a uno de los pilares del razonamiento matemático, solo necesitas dos ingredientes:
1. Plantearles actividades y retos que les inviten a pensar y razonar.
2. Proporcionarles, gracias a los materiales manipulativos un contexto lúdico y provocador que les anime a investigar y probar hipótesis.

Aunque hay decenas de materiales interesantes, yo siempre recomiendo uno:
El geoplano.
El geoplano es un material ideal para aprender geometría porque:

Pero es que, además:
Encontrar actividades ricas y, sobre todo, comprender qué objetivos matemáticos hay detrás de ellas, requiere conocimiento y dedicación.
Lo sé por experiencia propia. Me he pasado, literalmente, cientos de horas buscando y preparando actividades para el geoplano.
Un trabajo que he volcado en un curso online:
Geometría (y números) con el geoplano.
Una formación que te ahorrará mucho tiempo y te dará pautas claras de cómo usar esta excelente herramienta:
Geometría (y números) con el geoplano es un curso online con el que aprenderás:
Matrícula abierta hasta el 30 de noviembre de 2025
¿Qué hay dentro de este curso?
Una duda muy habitual con el geoplano
¿Para qué edades lo recomiendas?
Si los niños son capaces de colocar gomas elásticas en el tablero, ya pueden empezar a explorar las posibilidades del geoplano.
Aunque desde los 4 o 5 años los niños son capaces de construir figuras en un geoplano, creo que para esas edades tiene un uso un poco limitado.
Considero que el geoplano es verdaderamente útil a partir de 6 años y sin límite de edad. Tanto en Educación Primaria como en Secundaria o Bachillerato, es una excelente herramienta para comprender multitud de conceptos geométricos y numéricos.
¿Cómo saber si será un material adecuado para mis alumnos o mis hijos?
El geoplano se lleva usando desde hace 60 años y continúa siendo uno de los materiales imprescindibles para el aula ¿por algo será?
¿Por qué me he decidido a hacer este curso?
Porque los comentarios que recibía sobre el geoplano en otros cursos eran muy buenos
(y eso que solo le dedicaba una clase)
«Qué gran idea. Este curso voy a ser tutora del PQPI de carpintería, así que lo tenemos fácil para hacer un geoplano. Lo podremos trabajar en clase mientras los propios alumnos lo construyen en el taller. Mil gracias por esta idea. Genial»
HELENA. Docente
«¡Acabo de entender las áreas de las formas geométricas! Qué fácil, qué sencillo, qué lógico, qué bien se ve y cómo se entiende. Ha sido una clase maravillosa. Muchas gracias»
MARIA DEL CARMEN. Mamá.
«Muchas gracias Malena. Me encanta la manera que tienes de explicar. Así sí que se entienden las fórmulas que hasta ahora no tenían mucho sentido»
ARANTXA. Mamá y docente.
«Me encantó el geoplano, definitivamente lo voy a llevar a la práctica. Muchas gracias»
CLAUDIA. Docente.
«Esto de trabajar con geoplanos siempre me ha encantado. Gracias por compartir tantas estrategias para seguir usándolo en el aula»
GUADALUPE. Maestra.
Te acompaño en tu aprendizaje
Estoy segura de que te resultará fácil y ameno seguir el curso.
Por eso no tengo ningún miedo en comprometerme a responder cualquier duda que te surja hoy o dentro de diez años.
El curso online
Geometría (y números) con el geoplano
incluye
Matrícula abierta hasta el 30 de noviembre de 2025
¿Qué contenidos verás en el curso?
Clase 1: El geoplano
Clase 2: Primeras actividades
Clase 3: Líneas y ángulos
Clase 4: Polígonos
Clase 5: Transformaciones en el plano
Clase 6: Representación de figuras tridimensionales
Clase 6: Concepto de perímetro y área
Clase 7: Cálculo de áreas I
Clase 8: Cálculo de áreas II
Clase 9: Cálculo de áreas III
Clase 11: El geoplano circular
Clase 12: Ángulos y polígonos en un geoplano circular
Clase 13: Recorridos y patrones. Sistemas de coordenadas
Clase 14: Números
Clase 15: Operaciones aritméticas

Soy Malena Martín, matemática y formadora de docentes.
Será un placer acompañarte en el descubrimiento del geoplano.
«Excelentes estrategias para adentrarlos al mundo del área y del perímetro. Lo pondré en práctica con mis alumnos la semana que viene ya que es el tema que nos toca ver y sé que les encantará.
Gracias Malena»
ANA C. Maestra
«Lo explicas genial y tan sencillo que quiero volver a ser niña. Porque es verdad que me gustan las matemáticas y no se me daban nada mal, pero así es muy divertido y les ayuda a descubrir tantos conceptos [...]».
Mº JÉSSICA G. Mamá
Preguntas frecuentes
En este curso conocerás actividades para ayudar a tus niños a desarrollar el razonamiento geométrico. Para ello, solo necesitas una noción básica de matemáticas.
En las clases encontrarás el paso a paso de cada propuesta y si te surge alguna duda, podrás preguntarme.
Siempre apuesto por una formación de calidad, autónoma y consciente.
Por eso, en el curso no encontrarás tests ni trabajos para hacer-ver que aprendes. Aunque si lo solicitas te puedo extender un certificado, este curso no recibe subvenciones ni obligaciones de ninguna entidad pública ni privada.
Es más, cualquier formación que ofrezco, trato de que se parezca lo menos posible a una asignatura universitaria. Ya hemos hecho suficientes cursos que no nos han servido para nada.
Sí que tienes que hacer tareas y ejercicios, pero para comprender cómo trabajar con el geoplano.
Eso sí, no tendrás que demostrarme que aprendes, tú único supervisor será tu propio avance y tu día a día en el aula, en tu casa o en tu consulta.
Para realizar el curso es recomendable tener un geoplano. Mejor si tienes los tres modelos: isométrico, ortométrico y circular ya que las actividades que se pueden hacer con cada uno de ellos son diferentes.
Dicho esto, no es totalmente imprescindible ya que también puedes seguir las propuestas del curso con tramas de puntos dibujadas en un papel.
No se puede hablar de duración ya que el acceso a todo el contenido y a las consultas es ilimitado.
Verás que una vez matriculada tendrás acceso a todos los contenidos para que así puedas organizarte como creas conveniente.
El geoplano es uno de los materiales que siempre recomiendo para trabajar la geometría en Primaria y Secundaria. Por tanto, si tienes el curso Construimos matemáticas en Primaria o su hermano mayor, Construimos matemáticas en Secundaria, habrás visto que muestro algunas actividades con el geoplano.
Pero hay muchas más.
Precisamente, este curso nace de la necesidad de profundizar en un material muy presente en los colegios pero al que no se le da un uso apropiado.
En definitiva, aunque tengas uno de esos dos cursos, aquí aprenderás mucho más sobre el potencial del geoplano.
El pago se realiza mediante tarjeta bancaria de crédito o débito a través de una pasarela de pago segura. Solo tienes que hacer clic en el botón para apuntarte al curso y completar el pago como en cualquier tienda online.
Otras opciones de pago son transferencia bancaria y Paypal. Si vives fuera de España puedes pagar con Western Union. Si prefieres alguna de estas opciones de pago, escribe a cursos@aprendiendomatematicas.com
Los cursos están alojados en la Escuela online de Aprendiendo Matemáticas. Accederás a ella desde www.aprendiendomatematicas.com. Haciendo clic en el botón "Accede a tu curso" y después en la palabra Acceder.
Introduce tu correo y la contraseña que ya tengas o bien si es tu primer curso la que te haya llegado en el mensaje de «Tu cuenta ha sido creada» (una vez dentro la podrás editar desde tu perfil).
Si ya has hecho algún curso en nuestra Escuela, utiliza el mismo correo electrónico que tienes para acceder y así este curso aparecerá en tu área de alumna.
He decidido no comprometerme a próximas ediciones. ¿Por qué? Porque necesito tener más flexibilidad y libertad en mi calendario.
Eso no quiere decir que en 2025 no lance segunda edición de este curso. Como digo, ni confirmo ni desmiento.
Porque sé que el tiempo es un bien escaso, el curso tiene acceso ilimitado. Así no te agobias y lo haces a tu ritmo.
No solo es adecuado sino que yo diría especialmente adecuado.
Cuando cursé el Máster en Intervención en dificultades del aprendizaje, descubrí que, cuando existe un obstáculo específico para el aprendizaje, el uso de materiales manipulativos es imprescindible para que los niños avancen en cualquier aprendizaje, sobre todo, en matemáticas.
En particular, el geoplano es un material muy apropiado cuando presentan déficits motores (en el caso de dificultades muy severas se puede usar un geoplano virtual) o déficits visuales (se puede trabajar sin tener en cuenta los colores o bien identificar estos de manera táctil).
También están recomendados para TEA, AACC, TDAH, discapacidad intelectual o trastornos del desarrollo del lenguaje en la expresión oral.
El curso online
Geometría (y números) con el geoplano
incluye

© 2025 Aprendiendo Matemáticas - Malena Martín